11 Основні функції комплексної змінної
Нагадаємо визначення комплексної експоненти – . Тоді
Розкладання до ряду Маклорена. Радіус збіжності цього ряду дорівнює +∞, отже, комплексна експонента аналітична на всій комплексній площині і
(exp z) "=exp z; exp 0 = 1. (2)
Перша рівність тут випливає, наприклад, з теореми про почленное диференціювання статечного ряду.
11.1 Тригонометричні та гіперболічні функції
Синусом комплексного змінногоназивається функція

Косинус комплексного змінногоє функція

Гіперболічний синус комплексного змінноговизначається так:
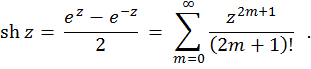
Гіперболічний косинус комплексного змінного- це функція

Відзначимо деякі властивості нововведених функцій.
A.Якщо x∈ ℝ cos cos, sin x, ch x, sh x∈ ℝ .
Б.Має місце наступний зв'язок тригонометричних та гіперболічних функцій:
cos iz = ch z; sin iz = ish z, ch iz = cos z; sh iz = isin z.
В. Основні тригонометричні та гіперболічні тотожності:
cos 2 z+sin 2 z=1; ch 2 z-sh 2 z = 1.
Доказ основної гіперболічної тотожності.
Основне тригонометричне тотожність випливає з оновленого гіперболічного тотожності при обліку зв'язку тригонометричних та гіперболічних функцій (див. властивість Б)
Г Формули додавання:
Зокрема,
Д.Для обчислення похідних тригонометричних та гіперболічних функцій слід застосувати теорему про почленное диференціювання статечного ряду. Отримаємо:
(cos z) "=-sin z; (sin z)" = cos z; (ch z) "= sh z; (sh z)" = ch z.
е.Функції cos z, ch z парні, а функції sin z, sh z непарні.
Ж. (Періодичність)Функція e z періодична з періодом 2π i. Функції cos z, sin z періодичні з періодом 2π, а функції ch z, sh z періодичні з періодом 2πi. Більш того,
Застосовуючи формули суми, отримуємо
З. Розкладання на дійсну та уявну частини:
Якщо однозначна аналітична функція f(z) відображає дію дію ділянку D на область G, то D називається областю однолистості.
І.Область D k =( x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Доведення. Зі співвідношення (5) випливає ін'єктивність відображення exp:D k → ℂ . Нехай w - будь-яке ненульове комплексне число. Тоді, розв'язуючи рівняння e x = | w | та e iy =w/|w| з дійсними змінними x і y (y вибираємо з напівінтерелу при п > 1 відмінна від нуля у всіх точках, крім z = 0. Записуючи у формулі (4) w і z у показовій формі отримуємо, що З формули (5) видно, що комплексні числа Z\ і z2 такі, що де k - ціле, переходять в одну точку w. сектор де а - будь-яке дійсне число. В області (7) відображення (4) є конформним. - багатозначна, тому що для кожного комплексного числа z = ге1в Ф 0 можна вказати п різних комплексних чисел, таких, що їх n-й ступіньдорівнює z: Зазначимо, що багаточлен ступеня п комплексного змінного z називається функція де задані комплексні числа, причому ао Ф 0. Багаточлен будь-якого ступеня є аналітичною функцією на всій комплексній площині. 2.3. Дробно-раціональна функція Дробно-раціональна функція називається функція виду де) - багаточлени комплексного змінного z. Дробно-раціональна функція аналітична у всій площині, крім тих точок, у яких знаменник Q(z) перетворюється на нуль. Приклад 3. Функція Жуковського__ аналітична у всій площині г, за винятком точки г = 0. З'ясуємо умови на область комплексної площини, при яких функція Жуковського, що розглядається в цій галузі, буде однолистою. М Нехай точки Z) та zj функція (8) переводить в одну точку. Тоді при ми отримуємо, що значить, для однолистості функції Жуковського необхідне і виконання умови Прикладом області, що задовольняє умові однолистості (9), є зовнішність кола |z| > 1. Так як похідна функції Жуковського Елементарні функції комплексного змінного Дробно-раціональні функції Ступінна функція Показова функція Логарифмічна функція Тригонометричні та гіперболічні функції відмінна від нуля усюди, крім точок, то відображення області здійснюване цією функцією, буде конформним. Зауважимо, що начинка одиничного кола |I також є областю однолистості функції Жуковського. Мал. 13 2.4. Показова функція Показову функцію ez визначимо для будь-якого комплексного числа z = х + гу наступним співвідношенням: При х = 0 отримуємо формулу Ейлера: Опишемо основні властивості показової функції: 1. Для дійсних z дане визначення збігається із звичайним. У цьому можна переконатися безпосередньо, поклавши у формулі (10) у = 0. 2. Функція ez аналітична на всій комплексній площині, і для неї зберігається нормальна формула диференціювання 3. Для функції ег зберігається теорема складання.
