The mathematical representation of the function shows visually how one value entirely determines the value of another value. Traditionally, the numeric functions that are put in touch with the other numbers. Zero functions, usually call the value of the argument at which the function adds to zero.
Instruction
1. In order to detect the zeros of the functions, it is necessary to equate its right-to-zero and solve the obtained equation. Imagine, you are given a function f (x) \u003d x-5.
2. To find the zeros of this function, take and equate its right side to zero: x-5 \u003d 0.
3. After deciding this equation, we obtain that X \u003d 5 and this value of the argument and will be zero functions. That is, with the value of the argument 5, the function f (x) appeals to zero.
Under the submission functions In mathematics, they understand the relationship between elements of sets. If we say more correctly, this "law", along which the whole element of one set (called the definition region) is put in accordance with a certain element of another set (called the area of \u200b\u200bthe values).
You will need
- Knowledge in the field of algebra and mathematical review.
Instruction
1. Values functions This is a certain area, the values \u200b\u200bof which can receive a function. Say the value area functions f (x) \u003d | x | from 0 to infinity. In order to detect value functions At a certain point you need to substitute argument functions its numeric equivalent, the resulting number and will value M. functions . Let the function f (x) \u003d | x | - 10 + 4X. Find value functions At point x \u003d -2. Substitute instead of X Number -2: F (-2) \u003d | -2 | - 10 + 4 * (- 2) \u003d 2 - 10 - 8 \u003d -16. I.e value functions At point -2 is -16.
Note!
Earlier than to look for the value of the function at the point - make sure it enters the function of defining the function.
Useful advice
A similar method is allowed to detect the value of the function of several arguments. The difference is that in return one number will need to substitute several - by the number of arguments of the function.
The function is the installed connection of the variable from the variable x. Moreover, the value of X, called the argument, corresponds to the exceptional value of the function. In graphical form, the function is depicted on a decartular coordinate system in the form of a graph. The intersection points of the graph with the abscissa axis on which the arguments are deposited x are called zeros of the function. Search for permissible zeros is one of the tasks of finding a given function. At the same time, all permissible values \u200b\u200bof the independent variable X forming the function of determining the function (OOOF) are taken into account.
Instruction
1. Zero function is such a value of the arodes of x, at which the function value is zero. However, only the arguments that are included in the field of determining the function under study can be. That is, in such a lot of values \u200b\u200bfor which the function f (x) has a sense.
2. Write down the specified function and equate it to zero, say f (x) \u003d 2x? + 5x + 2 \u003d 0. Decide the resulting equation and detect its valid roots. The roots of the square equation are calculated with the support of the discriminant. 2x? + 5x + 2 \u003d 0; d \u003d b? -4ac \u003d 5? -4 * 2 * 2 \u003d 9; x1 \u003d (-b +? D) / 2 * a \u003d (-5 + 3) / 2 * 2 \u003d -0.5; x2 \u003d (-b-? D) / 2 * a \u003d (-5-3) / 2 * 2 \u003d -2. In this case, two roots of the square equation corresponding to the initial function arguments were obtained f (x).
3. All detected x values \u200b\u200bcheck for belonging to the definition area of \u200b\u200bthe specified function. Discover the OOF, for this, check the initial expression on the presence of an even degree of type roots? F (x), to the presence of fractions in the function with an argument in the denominator, for the presence of logarithmic or trigonometric expressions.
4. Considering the function with the expression under the root of an even degree, take over the definition area all the arguments of which the values \u200b\u200bof which do not turn the feeding expression into a negative number (in front of the function does not make sense). Specify whether the function detected functions fall into a certain area of \u200b\u200bpermissible values \u200b\u200bx.
5. The denomoter of the fraction cannot appeal to zero, will investigantly eliminate the arguments of x that lead to such a result. For logarithmic values, only those values \u200b\u200bof the argument under which the expression itself is much zero. Zero functions that pay for the grocery expression in zero or a negative number must be discarded from the final result.
Note!
By finding the roots of the equation, extra roots may occur. Check it easy: Quite to substitute the obtained value of the argument to the function and make sure whether the function in zero appears.
Useful advice
Occasionally, the function is not expressed in an obvious form through its arguments, then it is easy to know that it represents this feature. An example of this can serve as the equation of a circle.
The values \u200b\u200bof the argument z. for which f.(z.) Turns to zero called. zero point. if a f.(a.) \u003d 0, then a - zero point.
ORD.Dot butnaz. zero ordern.
, if a
FCP can be represented as f.(z.) \u003d, where 
analytical function I. 
0.
In this case, in the decomposition of the function in a series of Taylor (43) the first n. coefficients are zero
=
=
Etc. Determine the order of zero for 
and (1 -COS z.) As z.
=
0
=
=
Zero 1 order
1 - COS. z.
=
=
zero 2 order
ORD. Dot z.
=
naz. infinitely remote pointand zero.functions f.(z.), if a f.(
) \u003d 0. Such a function is decomposed in a row on negative degrees z.
: f.(z.)
=
. If a
first n.
coefficients are zero, then we come to zero order n.
in an infinitely remote point: f.(z.)
= z.
-
n.
.
Isolated singular points are divided into: a) disposable singular points; b) poles ordern. ; at) significantly special points.
Dot but Naz. disposable special pointfunctions f.(z.) if z. 
a.
lim. f.(z.)
= with - Final .
Dot but Naz. polyce ordern.
(n.
1) Functions f.(z.) if the inverse function 
=
1/
f.(z.) has zero order n. At point but.This feature can always be represented as f.(z.)
=
where 
- analytical function and 
.
Dot but Naz. significantly special pointfunctions f.(z.) if z. 
a.
lim. f.(z.) does not exist.
Row Laurent.
Consider the case of the ring region of convergence r. < | z. 0 – a.| < R. with center at point but For function f.(z.). We introduce two new circles L. 1 (r.) I. L. 2 (R.) near the boundaries of the ring with a point z. 0 between them. We will make a split rings, on the edges of the cut by connecting the circle, moving to the one-connected area and in
cauchy Integral Formula (39) We obtain two integrals by variable Z
f.(z. 0)
=
+
,
(42)
where integration goes in opposite directions.
For integral in L. 1 Conditions | z. 0 – a. | > | z. – a. |, and for integral L. 2 Reverse Condition | z. 0 – a. | < | z. – a. |. Therefore, the factor 1 / ( z. – z. 0) Spread in a row (a) in the integral L. 2 and in a row (b) in the integral L. one . As a result, we get a decomposition f.(z.) in the annular region in row Laurent. on positive and negative degrees ( z. 0 – a.)
f.(z. 0)
=
A. n.
(z. 0 - A.) n.
(43)
where A. n.
=
=
;A. -N.
=
Planning for positive degrees (z. 0 - but) Naz. the right part A number of Laurent (a series of Taylor), and the decomposition of negative degrees is called. the main partrow of Laurent.
If inside the circle L. 1 There are no special points and the function analytic, then in (44) the first integral is zero on the Cauchy theorem and only the right part will remain in the decomposition of the function. Negative degrees in decomposition (45) appear only when analytically disappears within the inner circle and serve to describe a function near isolated singular points.
To build a row of Laurent (45) for f.(z.) You can calculate the decomposition coefficients for the general formula or use the decomposition of the elementary functions included in f.(z.).
The number of terms ( n.) The main part of the Laurent series depends on the type of high point: removing a special point
(n.
=
0)
; significantly special point
(n. 
);
polen. Order(n.
-
final).
and for f.(z.)
=
dot z.
= 0 removing a special pointbecause The main part is not. f.(z.)
=
(z.
-
) = 1 -
b) for f.(z.)
=
dot z.
= 0 -
Pole 1st order
f.(z.)
=
(z.
-
) =
-
c) for f.(z.) = e. 1 / z. dot z. = 0 - significantly special point
f.(z.)
=
e. 1 /
z. =
If a f.(z.) analytic in the area D. with the exception of m. Isolated singular points 
and | z. 1 |
< |z. 2 |
< . . . < |z. m. | then when decomposing a function in degrees z. The whole plane is divided into m. + 1 Ring | z. i. |
< | z.
| < | z. i. + 1 | And the Laurent series has a different view for each ring. When decomposition in degrees ( z.
–
z. i.
) Region of the convergence of the Laurent series is a circle | z.
–
z. i.
| < r.where r.
- Distance to the nearest high point.
Etc. Spread function f.(z.)
=
in a row of Laurent in degrees z. and ( z.
-
1).
Decision. Imagine the function in the form f.(z.)
= - z. 2
. We use the formula for the amount of geometric progression 
. In a circle | z |< 1 ряд сходится и f.(z.)
= - z. 2
(1 + z.
+ z. 2
+ z. 3
+ z. 4
+ . . .) = - z. 2
- z. 3
- z. four - . . . . Decomposition contains only right part. Let's go to the outer area of \u200b\u200bthe circle | z | \u003e 1. The function will be presenting as 
where 1 / | z.|
< 1, и получим разложение f.(z.)
= z.
=z.
+ 1 +
Because , decomposition of the function in degrees ( z.
-
1) has the form f.(z.)
= (z.
-
1) -1
+ 2 + (z.
-
1) for all 
1.
Etc. Decompose in a row of Laurent function f.(z.)
=
:
a) in degrees z. in a circle | z.|
< 1; b)
по степеням z.
ring 1.<
|z.|
< 3 ; c)
по степеням (z.
–
2). The presentation. Spider on the simplest fraction
=
=
+
=
.
From conditions z.
=1
A.
= -1/2 , z.
=3
B.
= ½.
but) f.(z.)
=
½ [ 
]
= ½ [ 
-(1/3)
], with | z.|<
1.
b) f.(z.)
= - ½ [ 
+
]
= -
(
), at 1< |z.|
< 3.
with) f.(z.)
=
½ [ 
]= -
½
[ 
]
=
=
- ½
= -
, with | 2 - z.|
< 1
This is a circle of radius 1 with the center at the point z. = 2 .
In some cases, power series can be reduced to the set of geometric progressions and after that it is easy to determine the region of their convergence.
Etc. Explore the convergence of the row
.
. . +
+
+
+
1
+ ()
+ ()
2
+ ()
3
+ . . .
Decision. This is the sum of two geometric progressions with q. 1
=
, q. 2 \u003d (). From the conditions of their convergence follows 
< 1 ,
< 1 или |z.|
> 1 , |z.|
< 2 , т.е. область сходимости ряда кольцо
1 < |z.|
< 2 .
2. Find zeros of functions.
f (x) at x 
.
Answer f (x) at x .
2) x 2\u003e -4x-5;
x 2 + 4x +5\u003e 0;
Let f (x) \u003d x 2 + 4x + 5 then we find such x at which f (x)\u003e 0,
D \u003d -4 no zeros.
4. Inequality systems. Inequalities and inequality systems with two variables
1) Many solutions of the inequalities system have the intersection of sets of inequalities included in it.
2) Many solutions of inequality f (x; y)\u003e 0 can be graphically portrayed on the coordinate plane. Usually a line given by the equation F (x; y) \u003d 0, breaks the plane into 2 parts, one of which is the solution of inequality. To determine which of parts, it is necessary to substitute the coordinates of an arbitrary point M (x0; u0), not lying on the line F (x; y) \u003d 0, into inequality. If f (x0; u0)\u003e 0, then the solution of the inequality is part of the plane containing the point M0. If f (x0; u0)<0, то другая часть плоскости.
3) Many solutions of the system of inequalities are the intersection of sets of inequalities included in it. Let, for example, a system of inequalities is asked:
.
For the first inequality, many solutions have a circle of radius 2 and centered at the beginning of the coordinates, and for the second half-plane, located above the direct 2x + 3ow \u003d 0. The multitude of solutions of this system is the intersection of these sets, i.e. semicircle.
4) Example. Solve the system of inequalities:
The solution of the 1st inequality is the set, the 2nd set (2; 7) and the third - the set.
The intersection of these sets is the interval (2; 3], which is many solutions of the inequalities system.
5. Resolution of rational inequalities by intervals
The method of intervals is based on the following property of twisted (X - a): point x \u003d α divides the numeric axis into two parts - to the right of the point α bounce (x-α)\u003e 0, and to the left of the point α (x-α)<0.
Let it be necessary to solve the inequality (X-α 1) (X-α 2) ... (x-α n)\u003e 0, where α 1, α 2 ... α n-1, α n - fixed numbers, among which no equal, and such that α 1< α 2 <...< α n-1 < α n . Для решения неравенства (x-α 1)(x-α 2)...(x‑α n)>0 by the method of intervals is applied as follows: the numbers α 1, α 2 ... α n-1, α n are applied to the numerical axis; In the interval to the right of the greatest of them, i.e. The numbers α n, put a sign "plus", in the next right to the left of the left interval sign "minus", then - the "plus" sign, then the "minus" sign, etc. Then the set of all solutions of inequality (X-α 1) (X-α 2) ... (x - α n)\u003e 0 will be the union of all the gaps in which the "plus" sign is put, and the set of solutions of inequality (X-α 1 ) (X - α 2) ... (x - α n)<0 будет объединение всех промежутков, в которых поставлен знак «минус».
1) The solution of rational inequalities (i.e. inequalities of the form 
P (x) q (x) where - polynomials) is based on the following property of a continuous function: if the continuous function adds to zero at points x1 and x2 (x1; x2) and between these points does not have other roots, then in the intervals (x1; x2) The function saves its sign.
Therefore, to find the intervals of the alignment of the function y \u003d f (x), all points in which the F (X) function appeals to zero or tolerates the gap is noted on the numerical straight line. These points break the numeric direct to several gaps, inside each of which the function f (x) is continuous and does not apply to zero, i.e. Saves a sign. To determine this sign, it is enough to find a function sign in any point of the gap of the numerical direct.
2) to determine the intervals of the symbol of the rational function, i.e. To solve rational inequality, we note on the numerical direct root of the numerator and the roots of the denominator, which, as well as the roots and points of the rational function of the rational function.
Interval inequality solutions
3. 
< 20.
Decision. The area of \u200b\u200bpermissible values \u200b\u200bis determined by the system of inequalities:
For function f (x) \u003d - 20. Find F (X):
where x \u003d 29 and x \u003d 13 are from.
f (30) \u003d - 20 \u003d 0.3\u003e 0,
f (5) \u003d - 1 - 20 \u003d - 10< 0.
Answer:. Basic methods for solving rational equations. 1) the simplest: they are solved by conventional simplifications - bringing to a common denominator, bringing such members and so on. Square equations AX2 + BX + C \u003d 0 are solved by ...
X varies on the interval (0,1], and decreases at the interval.
We see that adding n. To the argument x. does not change
the value of the function. The smallest different number
of n. There is thus this period SIN 2 x. .
Zero function. The value of the argument at which the function is 0, called zero ( root) Functions . The function may have several zeros. For example, a function y. = x. (x. + 1) (x. - 3) has three zero: x. = 0, x. = — 1, x. \u003d 3. Geometrically zero function – this is the abscissa point of intersection of the schedule function with the axis H. .
Figure 7 shows a graph of the function with zeros: x. = a. , x. = b. and x. = c. .
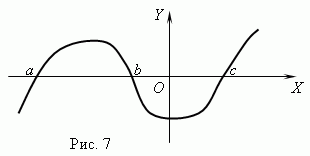
Asymptote. If the graph of the function is unlimited approaching some direct when its removal from the start of the coordinates, then this direct is called asimptoto.
Topic 6. "Interval Method".
If f (x) f (x 0) at x x 0, then the function f (x) is called continuous at point x 0.
If the function is continuous at each point of some gap i, then it is called continuous on the interval I (interval I call interval of continuity function). The graph of the function at this gap is a continuous line, which they say that it can be "drawing, without taking a pencil from paper."
Property of continuous functions.
If, on the interval (a; b), the function F is continuous and does not appeal to zero, then it remains a permanent sign on this interval.
On this property, the method of solving inequalities with one variable is based - the interval method. Suppose that the function f (x) is continuous on the interval I and turns to zero in the end number of points of this interval. By the property of continuous functions, these points I are divided into intervals, in each of which the continuous function f (x) C protects the permanent sign. To determine this sign, it is enough to calculate the value of the function f (x) at any one point from each such interval. Based on this, we obtain the following algorithm for the solution of inequalities by intervals.
Interval method for form inequalities
Interval method. Middle level.
Want to test your strength and find out the result How much are you ready for the exam or OGE?
Linear function
Linear is called the function of the form. Consider the function for example. It is positive at 3 "\u003e and negative when. Point is zero function (). Let's show the signs of this function on the numeric axis:
We say that "the function changes the sign when moving through the point."
It can be seen that the functions of the function correspond to the position of the function of the function: if the schedule is above the axis, the sign "", if below - "".
If we generalize the resulting rule on an arbitrary linear function, we obtain such an algorithm:
Quadratic function
I hope you remember how square inequalities are solved? If not, read the topic "Square inequalities". Let me remind you a general view of a quadratic function :.
Now let's remember which signs receive a quadratic function. Its graph - Parabola, and the function takes the sign "" with such in which Parabola is above the axis, and "" - if Parabola is below the axis:
If the function has zeros (the values \u200b\u200bin which), parabola crosses the axis at two points - the roots of the corresponding square equation. Thus, the axis is divided into three intervals, and the signs of the function alternately change when moving through each root.
Is it possible to somehow define signs without drawing every time a parabola?
Recall that the square three decrease can be decomposed on the factors:
Note roots on the axis:
We remember that the function sign can only change when moving through the root. We use this fact: for each of the three intervals to which the axis is divided with roots, it is enough to determine the function of the function only in one arbitrarily selected point: at the other points of the interval the sign will be the same.
In our example: at 3 "\u003e both expressions in brackets are positive (we substitute, for example: 0"\u003e). We put on the axis sign "":
Well, when (submits, for example,) both brackets are negative, it means that the work is positive:
That's what it is interval method: Knowing the signs of the factors at each interval, we define the sign of all the work.
Consider also cases when there is no zeros of the function, or it is only one.
If there are no, then there are no roots. So, there will be no "transition through the root". So, the function on the entire numeric axis takes only one sign. It is easy to determine, substituting into the function.
If the root is only one, the parabol is touched by the axis, so the function sign does not change when moving through the root. What rule will come up for such situations?
If you decompose such a function on multipliers, two identical multipliers will turn out:
And any expression in the square is nonnegative! Therefore, the function of the function does not change. In such cases, we will allocate the root, when moving through which the sign does not change, circled with a square:
Such root will be called multiple.
Interval method in inequalities
Now any square inequality can be solved without drawing a parabola. It is enough just to place the signs of the quadratic function on the axis, and select the intervals depending on the sign of inequality. For example:
Mind roots on the axis and lay signs:
We need part of the axis with the sign ""; Since the inequality of the unrest, the roots themselves are also included in the solution:
Now consider rational inequality - inequality, both parts of which are rational expressions (see "Rational Equations").
Example:
All factors except one - - here "linear", that is, contain a variable only in the first degree. Such linear multipliers are needed to apply the interval method - a sign when moving through their roots changes. But the multiplier does not have roots at all. This means that it is always positive (check it yourself), and therefore does not affect the sign of all inequality. It means that it can be divided by the left and right-hand side of the inequality, and thus get rid of it:
Now everything is the same as it was with square inequalities: we determine which points each of the multipliers turn to zero, mark these points on the axis and arrange signs. I pay attention very important fact:
In the case of an even number, we do the same as before: we supply the point by the square and do not change the sign when moving through the root. But in the case of an odd amount, this rule is not executed: the sign will still be changed during the transition through the root. Therefore, with such a root, we do not additionally do nothing, as if it is not a multiple. The above rules relate to all even and odd degrees.
What we write in the answer?
If there is a violation of the alternation of signs, it is necessary to be very attentive, because with incomprehensible inequality in response all painted points. But some of Nah often stand a mansion, that is, not included in the painted area. In this case, we add them to the answer as insulated points (in curly brackets):
Examples (Solving yourself):
Answers:
- If among the multipliers is simply a root, because it can be represented as.
.