11 Základní funkce komplexní proměnné
Připomeňme si definici komplexního exponenta -. Pak
Rozšíření řady Maclaurin. Poloměr konvergence této řady je + ∞, což znamená, že komplexní exponent je analytický na celé komplexní rovině a
(exp z) "\u003d exp z; exp 0 \u003d 1. (2)
První rovnost zde vyplývá například z věty o diferenciaci termínu po termínu pro výkonovou řadu.
11.1 Trigonometrické a hyperbolické funkce
Sinusová komplexní proměnná volal funkci

Kosinus komplexní proměnné existuje funkce

Hyperbolický sinus komplexní proměnné definováno takto:
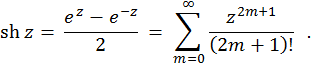
Hyperbolický kosinus složité proměnné je funkce

Všimněme si některých vlastností nově zavedených funkcí.
A.Pokud x∈ ℝ, pak cos x, sin x, ch x, sh x∈ ℝ.
B.Mezi trigonometrickými a hyperbolickými funkcemi existuje následující spojení:
cos iz \u003d ch z; sin iz \u003d ish z, ch iz \u003d cos z; sh iz \u003d isin z.
B. Základní trigonometrické a hyperbolické identity:
cos 2 z + sin 2 z \u003d 1; ch 2 z-sh 2 z \u003d 1.
Důkaz hlavní hyperbolické identity.
Hlavní trigonometrická identita vyplývá z hlavní hyperbolické identity při zohlednění spojení mezi trigonometrickými a hyperbolickými funkcemi (viz vlastnost B)
D Sčítací vzorce:
Zejména,
D. Pro výpočet derivátů trigonometrických a hyperbolických funkcí by měla být použita věta o diferenciaci výkonové řady po jednotlivých termínech. Dostaneme:
(cos z) "\u003d - sin z; (sin z)" \u003d cos z; (ch z) "\u003d sh z; (sh z)" \u003d ch z.
E.Funkce cos z, ch z jsou sudé a funkce sin z, sh z jsou liché.
G. (frekvence) Funkce e z je periodická s periodou 2π i. Funkce cos z, sin z jsou periodické s periodou 2π a funkce ch z, sh z jsou periodické s periodou 2πi. Navíc,
Použitím součtových vzorců získáme
Z. Rozklady na skutečnou a imaginární část:
Pokud jednohodnotová analytická funkce f (z) mapuje bijektivně doménu D na doménu G, pak D se nazývá doména univalence.
A.Doména D k \u003d (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Důkaz. Z relace (5) vyplývá, že mapování exp: D k → ℂ je injektivní. Nechť w je jakékoli nenulové komplexní číslo. Poté vyřešíme rovnice e x \u003d | w | a e iy \u003d w / | w | se skutečnými proměnnými x a y (y je vybráno z polovičního intervalu pro n\u003e 1 je nenulové ve všech bodech kromě z \u003d 0. Zápisem w a z v exponenciálním tvaru ve vzorci (4) získáme ze vzorce (5), že komplexní čísla Z \\ a z2 taková, že kde k je celé číslo, jsou mapována do jednoho bodu w. Proto pro n\u003e 1 není mapování (4) v rovině z univalentní. Nejjednodušší příklad domény, ve které je mapování z \u003d zn univalentní, je sektor, kde a je libovolné reálné číslo. V doméně (7) je mapování (4) konformní - s více hodnotami, protože pro každé komplexní číslo z \u003d r1 v Φ 0 lze zadat n různých komplexních čísel tak, aby jejich n-tý stupeň je rovno z: Všimněte si, že polynom stupně n komplexní proměnné z je funkce, kde jsou dána komplexní čísla, a ao Φ 0. Polynom libovolného stupně je analytická funkce na celé komplexní rovině. 2.3. Frakční racionální funkce Frakční racionální funkce je funkcí formy, kde) - komplex polynomů proměnná z. Frakční racionální funkce je analytická v celé rovině, s výjimkou těch bodů, ve kterých zmizí jmenovatel Q (z). Příklad 3. Žukovského funkce __ je analytická v celé rovině z, vyjma bodu r \u003d 0. Zjistíme podmínky v oblasti komplexní roviny, za které bude Zhukovského funkce uvažovaná v této oblasti jednotná. M Nechte body Z) a zj převzít funkcí (8) do jednoho bodu. Potom, protože, získáme, že pro univalenci Zhukovského funkce je tedy nutné a dostatečné splnit podmínku. Příkladem domény splňující podmínku univalence (9) je zevnějšek kruhu | z | \u003e 1. Jelikož derivace Zhukovského funkce Základní funkce komplexní proměnné Frakční racionální funkce Síla funkce Exponenciální funkce Logaritmická funkce Trigonometrické a hyperbolické funkce jsou nenulové všude, s výjimkou bodů, mapování oblasti prováděné touto funkcí bude konformní (obr.13). Všimněte si, že vnitřek disku jednotky | I je také doménou univalence Zhukovského funkce. Postava: 13 2.4. Exponenciální funkce Exponenciální funkce ez je definována pro libovolné komplexní číslo z \u003d x + zy následovně: Pro x \u003d 0 získáme Eulerův vzorec: Popíšeme hlavní vlastnosti exponenciální funkce: 1. Pro skutečné z se tato definice shoduje s obvyklou. To lze ověřit přímo nastavením y \u003d 0 ve vzorci (10). 2. Funkce ez je analytická v celé komplexní rovině a obvyklý diferenciační vzorec pro ni zůstává. 3. Veta sčítání je pro funkci e zachována. Dej 4. Funkce ez je periodická s imaginární hlavní periodou 2xi. Ve skutečnosti pro každé celé číslo k Na druhou stranu, pokud pak z definice (10) vyplývá, že odkud vyplývá, že, nebo kde n je celé číslo. Pás neobsahuje jedinou dvojici bodů spojených vztahem (12), proto z provedené studie vyplývá, že mapování w \u003d e "je v pruhu jednořádkové (obr. 14). Útočí jako derivace, toto mapování je konformní. Poznámka. Funkce rg je v libovolném pruhu univalentní 2.5 Logaritmická funkce Z rovnice, kde je uvedena, neznámá, získáme Proto Funkce, inverzní funkce je definována pro libovolný a je reprezentována vzorcem, kde Tato funkce s více hodnotami se nazývá logaritmická a je označována následovně Hodnota arg z se nazývá hlavní hodnota logaritmu a Pak získáme vzorec 2.6 pro Ln z. Trigonometrické a hyperbolické funkce Z Eulerova vzorce (11) pro skutečné y získáme Odkud Definujeme trigonometrické funkce sin z a cos z pro libovolné komplexní číslo z pomocí následujících vzorců: Sinus a kosinus komplexního argumentu mají zajímavé vlastnosti Uveďme ty hlavní: Funkce sinz a cos z: 1) pro skutečné x z-x se shoduje s obvyklými sinusy a kosiny; 2) jsou analytické v celé komplexní rovině; 3) dodržujte obvyklé vzorce diferenciace: 4) periodické s periodou 2 m; 5) sin z je lichá funkce a cos z je sudá; 6) obvyklé trigonometrické vztahy jsou zachovány. Všechny uvedené vlastnosti lze snadno získat ze vzorců (15). Funkce tgz a ctgz v komplexní doméně jsou definovány vzorci a hyperbolické funkce jsou definovány vzorci „Hyperbolické funkce úzce souvisí s trigonometrickými funkcemi. Toto spojení je vyjádřeno následujícími rovnostmi: Sinus a kosinus komplexního argumentu mají ještě jednu důležitou vlastnost: v komplexní rovině | \\ berou libovolně velké kladné Pomocí vlastností 6 a vzorců (18) získáme, že Elementární funkce komplexní proměnné Frakční racionální funkce Síla Funkce Exponenciální funkce Logaritmická funkce Trigonometrické a hyperbolické funkce Odtud Za předpokladu, že máme Příklad 4. Je snadné ověřit, že -4 Skutečně ,
