11 Basic functions of a complex variable
Let us recall the definition of the complex exponent -. Then
Maclaurin series expansion. The radius of convergence of this series is + ∞, which means that the complex exponent is analytic on the whole complex plane and
(exp z) "\u003d exp z; exp 0 \u003d 1. (2)
The first equality here follows, for example, from the term-by-term differentiation theorem for a power series.
11.1 Trigonometric and hyperbolic functions
Sine complex variable called the function

Cosine of a complex variable there is a function

Hyperbolic sine of a complex variable defined like this:
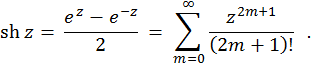
Hyperbolic cosine of a complex variable is a function

Let us note some properties of the newly introduced functions.
A.If x∈ ℝ, then cos x, sin x, ch x, sh x∈ ℝ.
B.There is the following connection between trigonometric and hyperbolic functions:
cos iz \u003d ch z; sin iz \u003d ish z, ch iz \u003d cos z; sh iz \u003d isin z.
B. Basic trigonometric and hyperbolic identities:
cos 2 z + sin 2 z \u003d 1; ch 2 z-sh 2 z \u003d 1.
Proof of the main hyperbolic identity.
The main trigonometric identity follows from the main hyperbolic identity when taking into account the connection between trigonometric and hyperbolic functions (see property B)
D Addition formulas:
In particular,
D. To calculate the derivatives of trigonometric and hyperbolic functions, the theorem on term-by-term differentiation of a power series should be applied. We get:
(cos z) "\u003d - sin z; (sin z)" \u003d cos z; (ch z) "\u003d sh z; (sh z)" \u003d ch z.
E.The functions cos z, ch z are even, and the functions sin z, sh z are odd.
G. (Frequency) The function e z is periodic with a period of 2π i. The functions cos z, sin z are periodic with a period of 2π, and the functions ch z, sh z are periodic with a period of 2πi. Moreover,
Applying the sum formulas, we obtain
Z. Decompositions into real and imaginary parts:
If a single-valued analytic function f (z) maps bijectively a domain D onto a domain G, then D is called a domain of univalence.
AND.Domain D k \u003d (x + iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции e z , которая отображает ее на область ℂ* .
Evidence. It follows from relation (5) that the mapping exp: D k → ℂ is injective. Let w be any nonzero complex number. Then, solving the equations e x \u003d | w | and e iy \u003d w / | w | with real variables x and y (y is chosen from a half-interval for n\u003e 1 is nonzero at all points except z \u003d 0. Writing w and z in exponential form in formula (4), we obtain from formula (5) that the complex numbers Z \\ and z2 such that where k is an integer are mapped to one point w. Hence, for n\u003e 1, mapping (4) is not univalent on the z plane. The simplest example of a domain in which the mapping z \u003d zn is univalent is sector where a is any real number. In the domain (7) the mapping (4) is conformal. - multivalued, since for each complex number z \u003d r1 in Φ 0 one can specify n different complex numbers such that their nth degree is equal to z: Note that a polynomial of degree n of a complex variable z is a function where are given complex numbers, and ao Φ 0. A polynomial of any degree is an analytic function on the entire complex plane. 2.3 Fractional rational function A fractional rational function is a function of the form where) - polynomials complex variable z. A fractional rational function is analytic in the entire plane, except for those points at which the denominator Q (z) vanishes. Example 3. Zhukovsky's function __ is analytic in the entire z-plane, excluding the point z \u003d 0. Let us find out the conditions on the region of the complex plane under which the Zhukovsky function considered in this region will be univalent. M Let the points Z) and zj be taken by function (8) to one point. Then, for, we obtain that Hence, for the univalence of the Zhukovsky function, it is necessary and sufficient to satisfy the condition. An example of a domain satisfying the univalence condition (9) is the exterior of the circle | z | \u003e 1. Since the derivative of the Zhukovsky function Elementary functions of a complex variable Fractional rational functions Power function Exponential function Logarithmic function Trigonometric and hyperbolic functions are nonzero everywhere, except for points, the mapping of the region carried out by this function will be conformal (Fig. 13). Note that the interior of the unit disc | I is also the univalence domain of the Zhukovsky function. Figure: 13 2.4. The exponential function The exponential function ez is defined for any complex number z \u003d x + zy as follows: For x \u003d 0 we obtain the Euler formula: Let us describe the main properties of the exponential function: 1. For real z, this definition coincides with the usual one. This can be verified directly by setting y \u003d 0 in formula (10). 2. The function ez is analytic on the entire complex plane, and the usual differentiation formula is preserved for it. 3. The addition theorem is preserved for the function e. We put 4. The function ez is periodic with an imaginary main period 2xi. Indeed, for any integer k On the other hand, if then from definition (10) it follows that whence it follows that, or where n is an integer. The strip does not contain a single pair of points connected by relation (12), therefore, from the performed study it follows that the mapping w \u003d e "is one-line in the strip (Fig. 14). As a derivative, this mapping is conformal. Remark. Function rg is univalent in any strip 2.5. Logarithmic function From the equation where the unknown is given, we obtain Hence, the function, the inverse of the function is defined for any and is represented by the formula where This multivalued function is called logarithmic and is denoted as follows. Then we obtain formula 2.6 for Ln z. Trigonometric and hyperbolic functions From Euler's formula (11) for real y we obtain Whence We define the trigonometric functions sin z and cos z for any complex number z by means of the following formulas: The sine and cosine of a complex argument have interesting properties Let us list the main ones: Functions sinz and cos z: 1) for real x z-x coincide with the usual sines and cosines; 2) are analytic on the whole complex plane; 3) obey the usual differentiation formulas: 4) are periodic with a period of 2m; 5) sin z is an odd function, and cos z is even; 6) the usual trigonometric relations are preserved. All the listed properties are easily obtained from formulas (15). The functions tgz and ctgz in the complex domain are defined by the formulas and hyperbolic functions are defined by the formulas "Hyperbolic functions are closely related to trigonometric functions. This connection is expressed by the following equalities: The sine and cosine of a complex argument have one more important property: on the complex plane | \\, they take arbitrarily large positive Using properties 6 and formulas (18), we obtain that Elementary functions of a complex variable Fractional rational functions Power function Exponential function Logarithmic function Trigonometric and hyperbolic functions Whence Assuming, we have Example 4. It is easy to verify that -4 Indeed ,
